
本文参考:
https://zhuanlan.zhihu.com/p/700455157
先学习下 UE 中八叉树的写法
TOctree2
首先 UE 中的八叉树是用来管理空间中的元素的,特殊的松散八叉树。每个节点存储若干“元素”,这些元素是完全被该节点包围盒包裹的元素。同时它还允许元素存在于有子节点的“分支节点上”,加入元素时如果该元素被子节点完全包裹就加入到子节点中,如果不能被任何一个子节点完全包裹,就加入到当前节点中,得益于松散八叉树,边缘的元素不会永久停留在某个中间节点内,更容易被加入到子节点。
数据结构
由于八叉树,总是以八个一组的节点分配内存,使用线性表来存储节点数据,建立内存池,分离树形结构和数据存储,有助于提高缓存命中率。
struct FNode
{
FNodeIndex ChildNodes = INDEX_NONE;
uint32 InclusiveNumElements = 0;
bool IsLeaf() const
{
return ChildNodes == INDEX_NONE;
}
};
FOctreeNodeContext RootNodeContext;
TArray<FNode> TreeNodes;
TArray<FNodeIndex> ParentLinks;
TArray<ElementArrayType> TreeElements;TreeNodes 存储节点基本数据,ParentLinks 存储每个节点组的父节点,TreeElements 存储每个节点存放的元素。
同样的文件中看到老版本的 TOctree,基本就是传统的实现方案。
空间测试
NodeContext 同来表示节点包围盒等空间特性的的类,提供包围检测、获取子节点 Context 等方法。
在八叉树中没有对某个节点随机访问其包围盒的需求,节点的包围盒仅仅是一种划分依据而非节点的固有数据。据此,不需要在每个节点内都存其空间属性。只需存一份 RootNodeContext 即可,无论是 AddElement、包围盒碰撞检测、查询点最近的元素等都是从根结点出发遍历的,因此只需要在遍历过程中递归计算子节点的包围盒即可。好处就是可以节省内存开销,坏处就是遍历时计算包围盒开销增大。
GetContainingChild
GetContainingChild 的方法是递归分割结点的依据,计算待测包围盒是否完全被哪个子节点包围。其思路是。先求出该中心点最邻近的包围盒与之比较,如果能被包围则输出该包围盒序号,否则不能被任何一个子节点包围。
这其中有个很 Trick 的问题我一度认为是出现 bug 了,我自己测试也是会得到错误的结果,就是我认为 MinDifference 应该取个绝对值,但实际不然原因如下。
FORCEINLINE FOctreeChildNodeRef FOctreeNodeContext::GetContainingChild(const FBoxCenterAndExtent& QueryBounds) const
{
FOctreeChildNodeRef Result;
// Load the query bounding box values as VectorRegisters.
const VectorRegister QueryBoundsCenter = VectorLoadAligned(&QueryBounds.Center);
const VectorRegister QueryBoundsExtent = VectorLoadAligned(&QueryBounds.Extent);
// Compute the bounds of the node's children.
const VectorRegister BoundsCenter = VectorLoadAligned(&Bounds.Center);
const VectorRegister ChildCenterOffsetVector = VectorLoadFloat1(&ChildCenterOffset);
//VectorSubtract和VectorAdd算出来的是八个子节点中心点的最大最小点,又与请求的包围盒中心点做了减法,
//看似得到的是两个向量。实际上基于八叉树节点是正方体和AABB这两个特性,八个子节点中心点,
//构成了一个内部正方体,以点在立方体内部为正,以下两个向量内实际存放的是,点到最小点所在的三个平面的x、y、z距离,
//以及点到最大点所在三个平面的x、y、z距离,这样用两个向量得到了,点到内部立方体六个面的情况。
const VectorRegister NegativeCenterDifference = VectorSubtract(QueryBoundsCenter,VectorSubtract(BoundsCenter,ChildCenterOffsetVector));
const VectorRegister PositiveCenterDifference = VectorSubtract(VectorAdd(BoundsCenter,ChildCenterOffsetVector),QueryBoundsCenter);
//如此这一步就很好理解了,两个向量求最小的x、y、z就是在求点最近的三个面的距离,实际上就是点到八个子节点中心最近点的向量。
//如果不好理解可以拆解到二维情况,或者是每个维度单独思考,这里各个维度可以看成独立的
// If the query bounds isn't entirely inside the bounding box of the child it's closest to, it's not contained by any of the child nodes.
const VectorRegister MinDifference = VectorMin(PositiveCenterDifference,NegativeCenterDifference);
//有了点到最近子节点的向量,只再需要加上包围盒的x、y、z扩展得到了其在x、y、z方向上的最远情况,再与子节点实际扩展范围比较即可
//这里有个很重要的特点,那就是我们假定请求的包围盒一定被大包围盒包裹,这也得益于该八叉树是向内松散的八叉树,
//因此这里的测试只需要考虑请求包围盒靠近中心的面与子节点的情况而无需考虑远离中心的面超过范围的问题。显然如果要保证请求包围盒,
//在子节点内,MinDifference应该加上绝对值,因为按照上面的定义,点在远平面外和小于近平面时,MinDifference呈现负数,画图可知,
//加上绝对值,MinDifference成为请求点到节点中心点的距离绝对值,在加Extent,就是在各个维度半径内的距离,再去和子节点Extent判断很合理。
//但是这里不需要这一步,以点在内部为正,即点在内部时,距离六个面距离都是正数,这样的特性让MinDifference+Extent始终等于靠近节点中心的面到节点中心点的距离,
//因此可以直接和子节点Extent做判断。
if(VectorAnyGreaterThan(VectorAdd(QueryBoundsExtent,MinDifference),VectorLoadFloat1(&ChildExtent)))
{
Result.SetNULL();
}
else
{
//到此我们依然不知道,这个最近的点是几号子节点。这个可以根据划分象限判断即可,QueryBoundsCenter-BoundsCenter的符号正负性,
//即可揭示请求包围盒在哪个象限,代码直接根据向量各部大小比较结果,再转换成掩码,取最后3位就得到了子节点索引。
// Return the child node that the query is closest to as the containing child.
Result.Index = VectorMaskBits(VectorCompareGT(QueryBoundsCenter, BoundsCenter)) & 0x7;
}
return Result;
}补一下上面的 MinDifference 的图
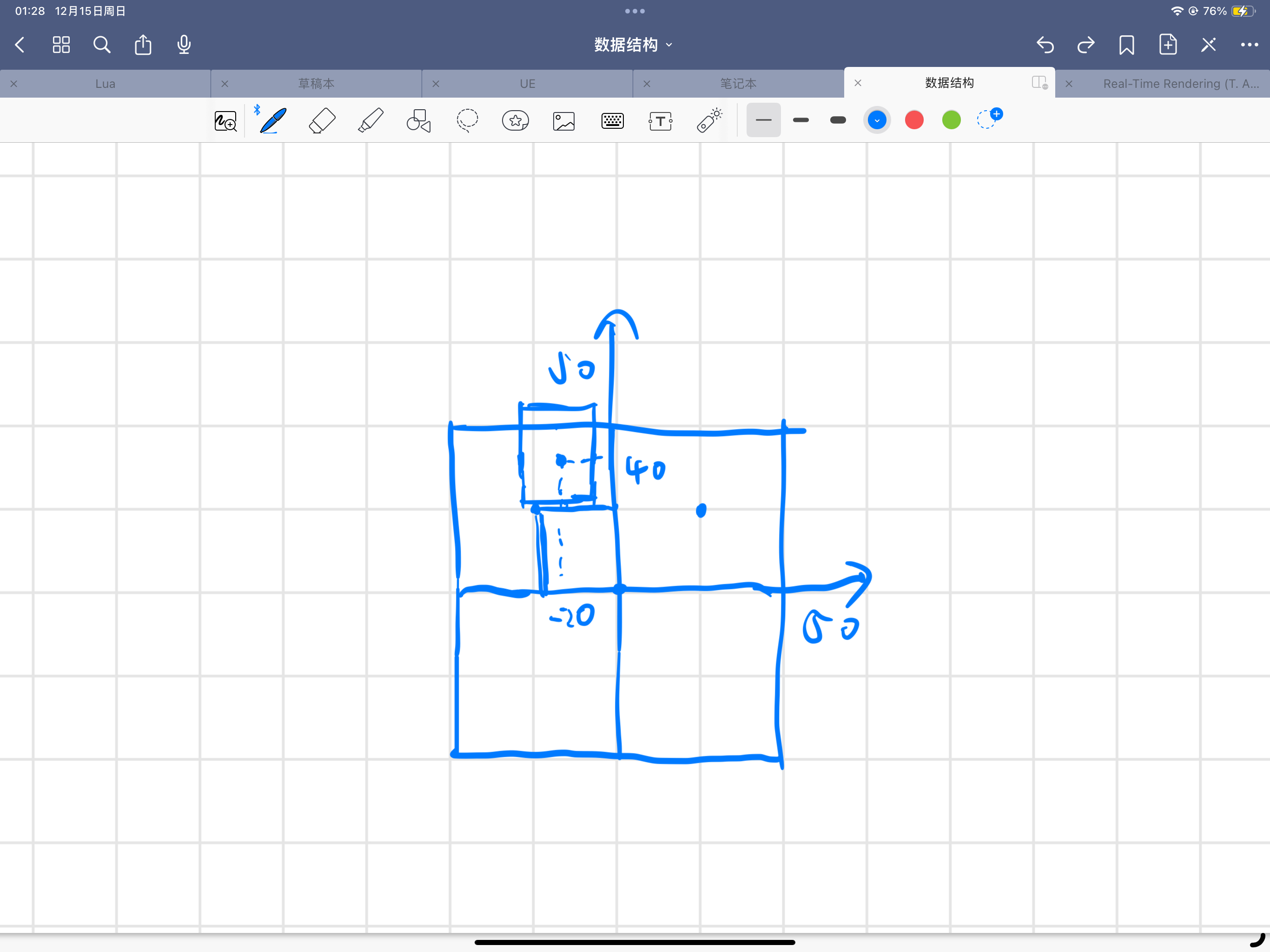
此时 MinDifference 的 y 在内正方形外侧应该是负的,加上 extent 依然不会越过外边界,但是实际上越过了,这种情况下,该函数也确实会返回错误的结果认为 querybox 在左上角节点内。由此也能看到内正外负的设计让 MinDifference+extent 这样的操作始终等于靠内边界与节点中心的距离。
GetIntersectingChildren
空间划分八叉树不一定需要测试包围盒属于那个子节点,更重要的是测试包围盒与哪些子节点相交,因此学习 GetIntersectingChildren 的写法。
在这个函数中比较关键的是设置了 FOctreeChildNodeSubset 这个子集来表示节点们。使用位的思路可以想到,子节点的索引使用三位 xyz,(0 代表-x,1 代表 +x)的节点这样 0-7 用三位二进制即可标明 8 个子节点。
若想表达节点集合,理论上需要八个二进制位,分别表示每个子节点的有无情况。但是 FOctreeChildNodeSubset 只用了 6 位,这里要结合算法来看。
比较重要的依然是隐含条件,那就是待测包围盒一定与当前大包围盒相交。主要思路就是,看待测包围盒在各个轴上“入侵”了哪些部分作为 Subset,由于宽松八叉树的存在需要计算出 6 个面来划分这八个子节点,PositiveChildBoundsMin 代表了 +x+y+z 部分子节点的 3 个平面,大于 PositiveChildBoundsMin 的话就代表“入侵”了 +x+y+z 的节点情况,NegativeChildBoundsMax 则代表了-x-y-z 部分节点情况。这里就能看到其思路依然去判断待测包围盒和节点内测分界面的关系,他不管外侧分界面,说白了就是画象限,如果不是松散八叉树 PositiveChildBoundsMin = NegativeChildBoundsMax = Bounds.Center,6 个分界面就退化成三个了,之后的测试函数就会基于这个修改。
这个算法只能在待测包围盒一定与当前大包围盒相交的情况下使用,如果包围盒完全在当前节点外侧那么得到的象限“入侵”状况就不能反应实际的相交情况了。
FORCEINLINE FOctreeChildNodeSubset FOctreeNodeContext::GetIntersectingChildren(const FBoxCenterAndExtent& QueryBounds) const
{
FOctreeChildNodeSubset Result;
// Load the query bounding box values as VectorRegisters.
const VectorRegister QueryBoundsCenter = VectorLoadAligned(&QueryBounds.Center);
const VectorRegister QueryBoundsExtent = VectorLoadAligned(&QueryBounds.Extent);
const VectorRegister QueryBoundsMax = VectorAdd(QueryBoundsCenter,QueryBoundsExtent);
const VectorRegister QueryBoundsMin = VectorSubtract(QueryBoundsCenter,QueryBoundsExtent);
// Compute the bounds of the node's children.
const VectorRegister BoundsCenter = VectorLoadAligned(&Bounds.Center);
const VectorRegister BoundsExtent = VectorLoadAligned(&Bounds.Extent);
const VectorRegister PositiveChildBoundsMin = VectorSubtract(
VectorAdd(BoundsCenter,VectorLoadFloat1(&ChildCenterOffset)),
VectorLoadFloat1(&ChildExtent)
);
const VectorRegister NegativeChildBoundsMax = VectorAdd(
VectorSubtract(BoundsCenter,VectorLoadFloat1(&ChildCenterOffset)),
VectorLoadFloat1(&ChildExtent)
);
//用最远的三个面去比+x+y+z三个情况,用最近的三个面去比-x-y-z三个情况,就得到Subset掩码了。
// Intersect the query bounds with the node's children's bounds.
Result.PositiveChildBits = VectorMaskBits(VectorCompareGT(QueryBoundsMax, PositiveChildBoundsMin)) & 0x7;
Result.NegativeChildBits = VectorMaskBits(VectorCompareLE(QueryBoundsMin, NegativeChildBoundsMax)) & 0x7;
return Result;
}
所以 Subset 本质上是要表示象限情况,利用象限交集截取子节点。由于都是长方体,假如他占据了顶部三个子节点,那一定也会占据第四个,所以有些情况是不存在的。使用 +x+y+z-x-y-z 共 6 位,表示每个轴上两个部分的包含情况,0 代表无,1 代表有。比如 + 部分和-部分互斥时,那说明该子集就表示那一个点,+x,-x 都为 1 时表示无论 x01 都包括,同时 +x,-x 不能同时为 0 那就说明该子集是个空集。
union
{
struct
{
uint32 bPositiveX : 1;
uint32 bPositiveY : 1;
uint32 bPositiveZ : 1;
uint32 bNegativeX : 1;
uint32 bNegativeY : 1;
uint32 bNegativeZ : 1;
};
struct
{
//拆分正部分和负部分,相交测试时快速赋值。
/** Only the bits for the children on the positive side of the splits. */
uint32 PositiveChildBits : 3;
/** Only the bits for the children on the negative side of the splits. */
uint32 NegativeChildBits : 3;
};
/** All the bits corresponding to the child bits. */
//有效位,同时为了快速判断Containing
uint32 ChildBits : 6;
/** All the bits used to store the subset. */
//为了快速置零
uint32 AllBits;
};有了这个基础后,要判断一个 Index 是否在 Subset 内只需分两步。
- 将 Index 转成 Subset
令 +x+y+z = Index
令-x-y-z = ~Index 即可
- 判断两个 Subset 的包容关系
设大集合 Sa 和待测集合 Si,Sa 包含 Si 的条件是,Sa 上各位 >=Si 上各位,即 Sa 为 0 时 Si 必须为 0,因此用 Sa 做掩码与 Si 判等。
FORCEINLINE bool FOctreeChildNodeSubset::Contains(FOctreeChildNodeRef ChildRef) const
{
// This subset contains the child if it has all the bits set that are set for the subset containing only the child node.
const FOctreeChildNodeSubset ChildSubset(ChildRef);
return (ChildBits & ChildSubset.ChildBits) == ChildSubset.ChildBits;
}直观说明待测包围盒一定与当前大包围盒相交前提
GetChildBox
最后再来看一下如何子节点的 Box,按照位运算的思路就是将索引的 01 情况直接去乘上偏移就能得到 center 的向量了,但实际做起来比较麻烦。
inline VectorRegister GetChildOffsetVec(int i) const
{
//用来做类型转换
union MaskType { VectorRegister v; VectorRegisterInt i;
} Mask;
Mask.v = MakeVectorRegister(1u, 2u, 4u, 8u);
VectorRegisterInt X = VectorIntLoad1(&i);
VectorRegisterInt A = VectorIntAnd(X, Mask.i);
Mask.i = VectorIntCompareEQ(Mask.i, A);
//这里1从int到float转换得到的结果不是1但是只要非0即可,因此用该算法可以这样转换。
return VectorSelect(Mask.v, VectorSetFloat1(ChildCenterOffset), VectorSetFloat1(-ChildCenterOffset));
}这里又用了很 trick 的技巧,使用 union 在两个不能转换的类型之间强制转换。先设计 4 个掩码来提取 Index 的各个位,用 VectorIntLoad1 把 Index 扩展了 4 次,与运算以后把得到的结果再做一个全等判断,就把 Index4 位,拆到了 m128 向量 4 个位置上了。最后把 int 的 1 转换到 float 实际上会得到一个错误的值但不会影响 VectorSelect 的结果。我实际想了下,如果用 m128i 和 m128 分开做还真不好做,这个类型强转确实巧妙,也得益于这里面的操作都是 0,1 两种情况。整理一下就得到获取子节点 Box 的方法了。
static FBoxCenterAndExtent GetChildBox(const FBoxCenterAndExtent& CurNode, FOctreeChildNodeRef ChildRef) {
float ChildOffset = CurNode.Extent.X / 2;
//用来做类型转换
union MaskType {
VectorRegister v; VectorRegisterInt i;
} Mask;
Mask.v = MakeVectorRegister(1u, 2u, 4u, 8u);
VectorRegisterInt X = VectorIntLoad1(&ChildRef.Index);
VectorRegisterInt A = VectorIntAnd(X, Mask.i);
Mask.i = VectorIntCompareEQ(Mask.i, A);
//这里1从int到float转换得到的结果不是1但是只要非0即可,因此用该算法可以这样转换。
VectorRegister ChildOffsetReg = VectorSelect(Mask.v, VectorSetFloat1(ChildOffset), VectorSetFloat1(-ChildOffset));
FBoxCenterAndExtent LocalBounds;
VectorRegister ZeroW = MakeVectorRegister(1.0f, 1.0f, 1.0f, 0.0f);
VectorStoreAligned(VectorMultiply(ZeroW, VectorAdd(VectorLoadAligned(&CurNode.Center), ChildOffsetReg)), &LocalBounds.Center);
VectorStoreAligned(VectorMultiply(ZeroW, VectorSetFloat1(ChildOffset)), &LocalBounds.Extent);
return LocalBounds;
}MyOctree
空间划分八叉树最大的区别在于,节点不是包围元素而是被元素分割,同时不是松散八叉树而是一般八叉树。
原理就是插入一个包围盒,如果是叶子节点就分割,检测他与哪些子节点相交,然后不断递归。
数据结构
学习 UE 的方法 8 个节点为一组分配内存。
//用来存储以8个节点为一组的ID。
using FNodeGroupIndex = int32;
using FNodeIndex = int32;
float MinExtent;
struct FNode
{
FNodeGroupIndex ChildIndex;
bool bIsValid;
//FNodeIndex NodeIndex = INDEX_NONE;
FNode() :ChildIndex(INDEX_NONE), bIsValid(true) {}
FNode(bool IsValid) :ChildIndex(INDEX_NONE), bIsValid(IsValid) {}
bool IsLeaf() const
{
return ChildIndex == INDEX_NONE;
}
};
struct FNodeData {
FBoxCenterAndExtent Bound;
TSet<FBlockID> Blocks;
bool bCanRun = true;
FNodeData(const FBoxCenterAndExtent& Bound) : Bound(Bound) {}
//FNodeData(){}
};
TArray<FNode> Nodes;//FNodeIndex -> FNode
TArray<FNodeIndex> Parents;//FNodeGroupIndex(child) -> FNodeIndex(parent)
TArray<FNodeData> NodeDatas;//FNodeIndex -> FNode
TArray<FNodeGroupIndex> FreeList;我这里为了清晰用了 FNodeGroupIndex 和 FNodeIndex 区分,ue 原本的代码区分不明显算来算去的。
FORCEINLINE FNodeIndex GroupToNodeIndex(FNodeGroupIndex Index) {
return Index * 8 + 1;
}
FORCEINLINE FNodeGroupIndex NodeToGroupIndex(FNodeIndex Index) {
return (Index - 1) / 8;
}因为我们这个树要在叶子节点上跑寻路算法,所以就把包围盒的情况加入到 FNodeData 中了,这个类似于 TreeElements。
然后是分配节点和释放结点的方法。这里我直接把子节点的 Box 算出来存储了,因为分配结点的时候可以少点拷贝。同时每个节点我还加了一个标志位 bIsValid 这个是为了后面收缩节点要用到的。
FNodeGroupIndex AllocateEightNodes(const FBoxCenterAndExtent& RootBound, FNodeIndex CurNode = INDEX_NONE) {
if (FreeList.Num() == 0) {
Nodes.AddDefaulted(8);
for (int i = 0; i < 8; i++) {
NodeDatas.Emplace(GetChildBox(RootBound, i));
}
return Parents.Add(CurNode);
}
else {
FNodeGroupIndex Result = FreeList.Pop();
for (int i = 0; i < 8; i++) {
NodeDatas[GroupToNodeIndex(Result) + i].Bound = GetChildBox(RootBound, i);
NodeDatas[GroupToNodeIndex(Result) + i].bCanRun = true;
NodeDatas[GroupToNodeIndex(Result) + i].Blocks.Empty();
Nodes[GroupToNodeIndex(Result) + i].ChildIndex = INDEX_NONE;
Nodes[GroupToNodeIndex(Result) + i].bIsValid = true;
}
return Result;
}
}
bool FreeEightNodes(FNodeGroupIndex GroupIndex) {
if (GroupIndex == INDEX_NONE) return false;
FNodeIndex Index = GroupToNodeIndex(GroupIndex);
for (int8 i = 0; i < 8; i++)
{
//Nodes[Index + i] = FNode(false);
//NodeDatas[Index + i] = FNodeData();
Nodes[Index + i].bIsValid = false;
}
Parents[GroupIndex] = INDEX_NONE;
FreeList.Add(GroupIndex);
return true;
}Block 管理
向树添加 Block。首先需要有一个 Map 来记录 Block 占据了哪些叶子节点,方便后面删除。一个 Block 池来获取 id,简单写了一个循环获取。
第一步先判断如果是叶子节点且如果能分割就分割,这里额外判断了如果当前点完全被 Block 包围那就没必要分割了。
第二步如果还是叶子节点的话那就直接把当前 BlockID 加入该节点,同时记录当前 NodeIndex 到 Map 中。
如果不是叶子节点,那么就要判断与哪些子节点相交了然后递归去添加即可。
TMap<FBlockID, TSet<FNodeIndex>> BlockNodes;
uint32 BlockIDCounter;
inline FBlockID GetNewBlockID() {
while (BlockNodes.Contains(++BlockIDCounter)) {}
return BlockIDCounter;
}
void AddBlockInternal(const FBoxCenterAndExtent& BlockBound, FBlockID BlockID, FNodeIndex CurNode) {
const FBoxCenterAndExtent CurBound = NodeDatas[CurNode].Bound;
if (Nodes[CurNode].IsLeaf() && CurBound.Extent.X >= MinExtent && !Contain(BlockBound, CurBound)) {
//TODO ????
FNodeGroupIndex NewGroupIndex = AllocateEightNodes(CurBound, CurNode);
Nodes[CurNode].ChildIndex = NewGroupIndex;
//Nodes[CurNode].ChildIndex = AllocateEightNodes(CurBound, CurNode);
Parents[NewGroupIndex] = CurNode;
}
if (Nodes[CurNode].IsLeaf()) {
NodeDatas[CurNode].bCanRun = false;
NodeDatas[CurNode].Blocks.Add(BlockID);
BlockNodes[BlockID].Add(CurNode);
}
else {
FChildNodeSubset Subset = GetIntersectingChild(CurBound, BlockBound);
for (int i = 0; i < 8; i++) {
if (Subset.Contains(i)) {
AddBlockInternal(BlockBound, BlockID, GroupToNodeIndex(Nodes[CurNode].ChildIndex) + i);
}
}
}
}
移除 Block 前先写收缩节点的方法。
从子节点向上收缩时,如果是叶节点,直接向上递归。如果有子节点,那么收缩的条件是,八个子节点的通行情况完全一致,比如都被 Block 或者都可通行。收缩时将所有子节点的 BlockID 添加到当前点同时更新 BlockNodes 这个 Map 的情况,并释放节点组。如果能收缩就继续向上递归。
inline bool IsNodeValid(FNodeIndex CurNode) {
return CurNode != INDEX_NONE && CurNode < Nodes.Num() && Nodes[CurNode].bIsValid;
}
//ShrinkFromBottom
void ShrinkUpNodeInternal(FNodeIndex CurNode) {
if (Nodes[CurNode].IsLeaf()) {
if (CurNode != 0) ShrinkUpNodeInternal(Parents[NodeToGroupIndex(CurNode)]);
}
else {
FNodeIndex Childs = GroupToNodeIndex(Nodes[CurNode].ChildIndex);
bool bCanShrink = true;
bool bRunState = NodeDatas[Childs].bCanRun;
for (int8 i = 0; i < 8; i++) {
if (!Nodes[Childs + i].IsLeaf() || NodeDatas[Childs + i].bCanRun != bRunState) {
bCanShrink = false;
break;
}
}
if (bCanShrink) {
for (int8 i = 0; i < 8; i++) {
for (FBlockID Block : NodeDatas[Childs + i].Blocks) {
BlockNodes[Block].Remove(Childs + i);
BlockNodes[Block].Add(CurNode);
}
NodeDatas[CurNode].Blocks.Append(NodeDatas[Childs + i].Blocks);
}
NodeDatas[CurNode].bCanRun = bRunState;
FreeEightNodes(Nodes[CurNode].ChildIndex);
Nodes[CurNode].ChildIndex = INDEX_NONE;
if (CurNode != 0) ShrinkUpNodeInternal(Parents[NodeToGroupIndex(CurNode)]);
}
}
}最后 RemoveBlock 就根据 FBlockID 将所有的占据的节点向上收缩即可,这里就需要 IsNodeValid 了,因为在收缩其他节点的时候会将兄弟八个节点一起收缩,遍历到后面的节点都已经收缩过了所以需要判断下。
bool RemoveBlock(FBlockID Block) {
if (!BlockNodes.Contains(Block)) return false;
for (FNodeIndex NodeIndex : BlockNodes[Block]) {
NodeDatas[NodeIndex].Blocks.Remove(Block);
if (NodeDatas[NodeIndex].Blocks.Num() == 0) {
NodeDatas[NodeIndex].bCanRun = true;
}
}
for (FNodeIndex NodeIndex : BlockNodes[Block]) {
if(IsNodeValid(NodeIndex)) ShrinkUpNodeInternal(NodeIndex);
}
BlockNodes.Remove(Block);
return true;
}空间测试
包围测试
static bool Contain(const FBoxCenterAndExtent& A, const FBoxCenterAndExtent& B) {
VectorRegister CenterA = VectorLoadAligned(&A.Center);
VectorRegister ExtentA = VectorLoadAligned(&A.Extent);
VectorRegister CenterB = VectorLoadAligned(&B.Center);
VectorRegister ExtentB = VectorLoadAligned(&B.Extent);
return VectorAnyGreaterThan(VectorAbs(VectorSubtract(CenterA, CenterB)), VectorSubtract(ExtentA, ExtentB)) == 0;
}测试两个 AABB 包围很简单,两个中心点的距离在 xyz 分量上不超过两个包围盒 Extent 的差即可。类似的测试两个 AABB 相交就是两个中心点的距离在 xyz 分量上不超过两个包围盒 Extent 的和。
GetChildBox
抄 UE 源码,上面介绍了。实际上,这里多做几个判断,根据 ChildRef 的位情况加上偏移就可以,不过 UE 这里这样做一方面是为了 SIMD 加速,另一方面是不用 IF 减少分支流,这应该是对于 GPU 比较友好。
static FBoxCenterAndExtent GetChildBox(const FBoxCenterAndExtent& CurNode, int32 ChildRef) {
float ChildOffset = CurNode.Extent.X / 2.f;
//用来做类型转换
union MaskType {
VectorRegister v; VectorRegisterInt i;
} Mask;
Mask.v = MakeVectorRegister(1u, 2u, 4u, 8u);
VectorRegisterInt X = VectorIntLoad1(&ChildRef);
VectorRegisterInt A = VectorIntAnd(X, Mask.i);
Mask.i = VectorIntCompareEQ(Mask.i, A);
//这里1从int到float转换得到的结果不是1但是只要非0即可,因此用该算法可以这样转换。
VectorRegister ChildOffsetReg = VectorSelect(Mask.v, VectorSetFloat1(ChildOffset), VectorSetFloat1(-ChildOffset));
FBoxCenterAndExtent LocalBounds;
VectorRegister ZeroW = MakeVectorRegister(1.0f, 1.0f, 1.0f, 0.0f);
VectorStoreAligned(VectorMultiply(ZeroW, VectorAdd(VectorLoadAligned(&CurNode.Center), ChildOffsetReg)), &LocalBounds.Center);
VectorStoreAligned(VectorMultiply(ZeroW, VectorSetFloat1(ChildOffset)), &LocalBounds.Extent);
return LocalBounds;
}GetIntersectingChild
抄 UE 源码,上面介绍了。
static FChildNodeSubset GetIntersectingChild(const FBoxCenterAndExtent& RootBound, const FBoxCenterAndExtent& QueryBound) {
FChildNodeSubset Result;
const VectorRegister QueryBoundsCenter = VectorLoadAligned(&QueryBound.Center);
const VectorRegister QueryBoundsExtent = VectorLoadAligned(&QueryBound.Extent);
const VectorRegister QueryBoundsMax = VectorAdd(QueryBoundsCenter, QueryBoundsExtent);
const VectorRegister QueryBoundsMin = VectorSubtract(QueryBoundsCenter, QueryBoundsExtent);
const VectorRegister BoundsCenter = VectorLoadAligned(&RootBound.Center);
Result.PositiveChildBits = VectorMaskBits(VectorCompareGT(QueryBoundsMax, BoundsCenter)) & 0x7;
Result.NegativeChildBits = VectorMaskBits(VectorCompareLE(QueryBoundsMin, BoundsCenter)) & 0x7;
return Result;
}GetPointInChild
根据点在八个象限的情况组成的掩码。
int GetPointInChild(const FVector& Point, FNodeIndex Node) {
VectorRegister Center = VectorLoadAligned(&NodeDatas[Node].Bound.Center);
VectorRegister PointVec = VectorLoadFloat3_W0(&Point);
return VectorAnyGreaterThan(PointVec, Center);
}HitTestWithLineInternal
线段的射线检测,这个比较麻烦,UE 那边也没有写。我也没想到什么比较好的不用 IF 的方法。直线和 AABB 求交点基本就是算各个面的进入和离开时间,这个参考 Games101 和其他的都有介绍。我这里写一个不用 0-7 循环判断每个子节点的方法。
首先前面的空间函数都做了假定,这里也可以做一个假定,Start 和 End 都在当前大包围盒内。
这样我们只需要算直线到中间三个分割面的情况,从 Start 出发,先穿过哪个面就进入哪个子节点,以此类推。
Center 向量本身就代表中间三个面,直接计算出 T。
T.X 就代表穿过 X 平面的时间。把 T 的三个分量排序。
这里 Mask 是用来标记 XYZ 的。
排序后,先获取 Start 属于的子节点标号,然后开始出发如果 T 在 0-1 之间说明是正常的可以进行判断。Index ^= MinMask 这一步可以将 Index 的 Mask 位 01 切换,代表节点穿过那个面进入后的 Index。递归判断时用截取后的 Start、End 就保证了 Start、End 一定属于当前大节点。
每进行一步就判断结果提前返回,这样 OutResult 中最后存下来的就是从 Start 出发第一个碰到的点。
这个函数参数应该写成 RayStart 和 RayDir,这里面有些重复计算比如 NormalDir,不过懒得改了。。。
bool HitTestWithLineInternal(FVector Start, const FVector& End, FNodeIndex Node, FVector& OutResult) {
if (Nodes[Node].IsLeaf()) {
OutResult = Start;
//UKismetSystemLibrary::DrawDebugBox(o, NodeDatas[Node].Bound.Center, NodeDatas[Node].Bound.Extent, FColor::Green);
return !NodeDatas[Node].bCanRun;
}
const FVector Center(NodeDatas[Node].Bound.Center);
const FVector Dir = End - Start;
const FVector NormalDir = Dir.GetSafeNormal();
//在平面上时无法判断加入补偿
if (FMath::IsNearlyEqual(Start.X, Center.X, 0.015f)) Start.X += NormalDir.X;
if (FMath::IsNearlyEqual(Start.Y, Center.Y, 0.015f)) Start.Y += NormalDir.Y;
if (FMath::IsNearlyEqual(Start.Z, Center.Z, 0.015f)) Start.Z += NormalDir.Z;
FVector StartVector = Start - Center;
const FVector T = - StartVector / Dir;
float MinT;
uint32 MinMask;
float MaxT;
uint32 MaxMask;
if (T.X < T.Y) {
MinT = T.X;
MinMask = 0b001;
MaxT = T.Y;
MaxMask = 0b010;
}
else {
MinT = T.Y;
MinMask = 0b010;
MaxT = T.X;
MaxMask = 0b001;
}
if (T.Z < MinT) {
MinT = T.Z;
MinMask = 0b100;
}
if (T.Z > MaxT) {
MaxT = T.Z;
MaxMask = 0b100;
}
//不能这么写因为T有可能是Inf/Nan
//float MidT = T.X + T.Y + T.Z - MaxT - MinT;
uint32 MidMask = 0b111 ^ MinMask ^ MaxMask;
float MidT = T[MidMask>>1];
FNodeIndex Child = GroupToNodeIndex(Nodes[Node].ChildIndex);
uint32 Index = (StartVector.X > 0) | ((StartVector.Y > 0) << 1) | ((StartVector.Z > 0) << 2);
bool HitResult = false;
FVector CurStart = Start;
if (MinT >= 0 && MinT <= 1) {
HitResult = HitTestWithLineInternal(CurStart, Start + MinT * Dir, Child + Index, OutResult);
Index ^= MinMask;
CurStart = Start + MinT * Dir;
}
if (HitResult) return HitResult;
if (MidT >= 0 && MidT <= 1) {
HitResult = HitTestWithLineInternal(CurStart, Start + MidT * Dir, Child + Index, OutResult);
CurStart = Start + MidT * Dir;
Index ^= MidMask;
}
if (HitResult) return HitResult;
if (MaxT >= 0 && MaxT <= 1) {
HitResult = HitTestWithLineInternal(CurStart, Start + MaxT * Dir, Child + Index, OutResult);
CurStart = Start + MaxT * Dir;
Index ^= MaxMask;
}
if (HitResult) return HitResult;
return HitTestWithLineInternal(CurStart, End, Child + Index, OutResult);
}
建图
叶子节点
首先要获取所有的叶子节点。为了外部使用方便所有的编号经过转换从头开始了。深搜即可,用一个 LeafMap 来记录叶节点编号的转换。
TMap<FNodeIndex, int32> LeafMap;
void GetLeafNodesInternal(TArray<FLeafNode>& LeafNodes, FNodeIndex CurNode, bool bAllowBlocked = true) {
if (Nodes[CurNode].IsLeaf()) {
if (bAllowBlocked || NodeDatas[CurNode].bCanRun) {
LeafNodes.Emplace(NodeDatas[CurNode].Bound, NodeDatas[CurNode].bCanRun);
LeafMap.Add(CurNode, LeafNodes.Num() - 1);
}
}
else {
for (int i = 0; i < 8; i++) {
GetLeafNodesInternal(LeafNodes, GroupToNodeIndex(Nodes[CurNode].ChildIndex) + i, bAllowBlocked);
}
}
}连接
连接叶子节点我看网上基本是给所有的叶子节点二重循环,设置一个最大距离,然后根据射线检测的结果决定是否相连的,这样的时间复杂度是 O(n2),而且边太多了,在复杂场景中占用的内存会比较大,不过好处就是这样一来直接用 A*就可以得到比较好的结果,寻路时的开销少一些。
我考虑了另一个思路能不能按照节点的相邻关系来连接,如果两个可通行节点相邻就认为他是连接的。在一个大节点内的 8 个子节点,可以按照 X、Y、Z 三个平面分别相连,以 X 平面为例,-X 的 4 个节点和 +X 的 4 个节点,面对面的两个节点相连一共 4 对。其他两个平面同理。
具体链接两个节点的方法,根据一个 Mask,比如两个节点按照 X 平面连接,那么 Mask 的 X 位(0 位)为 1,将-X 节点的 +X4 个子节点和 +X 节点的 4 个-X 节点相连即可。
连接大节点内的函数中,先把 8 个子节点两两连接,再把八个子节点内部连接。
void ConnectNode(TArray<TArray<TPair<int32, float>>>& Graph, FNodeIndex Node) {
if (Nodes[Node].IsLeaf()) return;
FNodeIndex Child = GroupToNodeIndex(Nodes[Node].ChildIndex);
uint32 Mask = 1;
for (uint32 i = 0; i < 3; i++) {
for (uint32 j = 0; j < 4; j++) {
uint32 Code = (j & (Mask - 1)) | ((j & (~(Mask - 1))) << 1);
ConnectNode(Graph, Code + Child, (Code | Mask) + Child, Mask);
}
Mask <<= 1;
}
for (uint32 i = 0; i < 8; i++) {
ConnectNode(Graph, Child + i);
}
}连接两个节点的函数中,如果两个节点都是叶子节点那就直接相连。
如果其中一个是叶子,那就将它与另一个节点依据 Mask 筛出来的 4 个节点相连。
如果两个都不是叶子,就依据 Mask,跟之前一样面对面两两相连。
这里 Node = (j & (Mask - 1)) | ((j & (~(Mask - 1))) << 1);可以根据 Mask 拼接两部分数。做了一个固定 Mask 位为 1 的一个循环遍历。这样不用遍历 8 次判断,可以直接遍历 4 次,拼出结果。
void ConnectNode(TArray<TArray<TPair<int32, float>>>& Graph, FNodeIndex NodeA, FNodeIndex NodeB, uint32 Mask) {
//FChildNodeSubset SubsetA(0b111, (~Mask) & 0x7);
//FChildNodeSubset SubsetB((~Mask) & 0x7, 0b111);
if (Nodes[NodeA].IsLeaf() && Nodes[NodeB].IsLeaf()) {
if (!NodeDatas[NodeA].bCanRun || !NodeDatas[NodeB].bCanRun) return;
float Distance = Dist(NodeA, NodeB);
Graph[LeafMap[NodeA]].Add(TPair<int32, float>{LeafMap[NodeB], Distance});
Graph[LeafMap[NodeB]].Add(TPair<int32, float>{LeafMap[NodeA], Distance});
return;
}
if (Nodes[NodeA].IsLeaf()) {
if (!NodeDatas[NodeA].bCanRun) return;
for (uint32 j = 0; j < 4; j++) {
uint32 Node = (j & (Mask - 1)) | ((j & (~(Mask - 1))) << 1);
ConnectNode(Graph, NodeA, GroupToNodeIndex(Nodes[NodeB].ChildIndex) + (Node), Mask);
}
return;
}
if (Nodes[NodeB].IsLeaf()) {
if (!NodeDatas[NodeB].bCanRun) return;
for (uint32 j = 0; j < 4; j++) {
uint32 Node = (j & (Mask - 1)) | ((j & (~(Mask - 1))) << 1);
ConnectNode(Graph, GroupToNodeIndex(Nodes[NodeA].ChildIndex) + (Node | Mask), NodeB, Mask);
}
return;
}
for (uint32 j = 0; j < 4; j++) {
uint32 Node = (j & (Mask - 1)) | ((j & (~(Mask - 1))) << 1);
ConnectNode(Graph, GroupToNodeIndex(Nodes[NodeA].ChildIndex) + (Node | Mask), GroupToNodeIndex(Nodes[NodeB].ChildIndex) + (Node), Mask);
}
}得到的结果如下,看起来还不错。他的总遍历次数实际上是对所有的分割面进行访问只访问了 1 次,这样时间复杂度只有 O(n),而且没有射线检测。

起点与终点
起点与终点应该如何加入到图里,我主要想了三种方法,第一种直接判断点在那个叶子中,然后与叶子中心点相连。这种方法最快,但是实际测下来无论是 Theta *还是 A*+ 平滑都不能很好处理这个起终点的锐角拐弯的问题,原因就是起终点连的点太少了,又想马儿跑得快又想马儿不吃草是不行的。所以另一个方法是,将起点终点转化为一个包围盒,将他所有碰撞到的叶子节点连接起来。进一步延伸,干脆把这个包围盒加入到树中去,然后重新生成一遍图。这里我直接实现第二种。
void AMyOctreeActor::BuildGraph()
{
if (bComplexGraph) Octree->GenerateComplexGraph(LeafNodes, Graph);
else Octree->GenerateGraph(LeafNodes, Graph);
LeafNodes.AddDefaulted(2);
Graph.AddDefaulted(2);
}这里面实际上还有很多思路,比如可以给起点终点遍历所有的叶子节点做 hittest 连接,因为这里拿到所有碰撞节点的结果也要做 hittest 来防止穿过障碍。
void AMyOctreeActor::AddStartAndEnd(const FVector& Start, const FVector& End, float Extent)
{
StartLeaves.Reset();
EndLeaves.Reset();
int32 StartIndex = LeafNodes.Num() - 2;
int32 EndIndex = LeafNodes.Num() - 1;
FBoxSphereBounds Bound(Start, FVector(Extent), 0);
LeafNodes[StartIndex].bCanRun = true;
LeafNodes[StartIndex].Bound = Bound;
Octree->GetIntersactingLeaves(Bound, StartLeaves);
Bound.Origin = End;
LeafNodes[EndIndex].bCanRun = true;
LeafNodes[EndIndex].Bound = Bound;
Octree->GetIntersactingLeaves(Bound, EndLeaves);
for (int32 Node : StartLeaves) {
FVector HitResult;
if (!Octree->HitTestWithLine(Start, LeafNodes[Node].Bound.Origin, HitResult)) Graph[StartIndex].Emplace(Node, FVector::Dist(Start, LeafNodes[Node].Bound.Origin));
}
for (int32 Node : EndLeaves) {
FVector HitResult;
if (!Octree->HitTestWithLine(End, LeafNodes[Node].Bound.Origin, HitResult)) Graph[Node].Emplace(EndIndex, FVector::Dist(End, LeafNodes[Node].Bound.Origin));
}
}寻路
A*
基本的 A*算法实现
struct FAStarNode {
int32 Index;
int32 Parent;
float CurCost;
float TotalCost;
bool bLazyTheta = false; //Only For LazyThetaStar
bool operator<(const FAStarNode& Other) const {
return TotalCost < Other.TotalCost;
}
};
TArray<FAStarNode> OpenList;
struct FPathNode {
int32 Parent;
float Cost;
};
TMap<int32, FPathNode> CloseSet;
void AMyOctreeActor::RunAStar()
{
int Num = LeafNodes.Num();
const FVector& Start = LeafNodes[Num - 2].Bound.Origin;
const FVector& End = LeafNodes[Num - 1].Bound.Origin;
OpenList.Reset();
CloseSet.Reset();
OpenList.HeapPush({ Num - 2 , Num - 2, 0, FVector::Dist(Start, End)});
while (OpenList.Num() > 0) {
FAStarNode CurNode;
OpenList.HeapPop(CurNode, false);
if (CloseSet.Contains(CurNode.Index)) continue;
CloseSet.Add(CurNode.Index, { CurNode.Parent, CurNode.CurCost });
if (CurNode.Index == Num - 1) break;
for (TPair<int32, float>& Line : Graph[CurNode.Index]) {
if (CloseSet.Contains(Line.Key)) continue;
float CurCost = CurNode.CurCost + Line.Value;
OpenList.HeapPush({ Line.Key , CurNode.Index, CurCost, CurCost + FVector::Dist(LeafNodes[Line.Key].Bound.Origin, End) });
}
}
}Theta*
Theta*是在 A* 搜索的过程中把当前点的相邻点加入后,判断这些相邻点是否与父节点能直接相连,相当于多考虑了一组路径。
void AMyOctreeActor::RunThetaStar()
{
#ifdef DEBUG_ALGORITHM
int32 Count = 0;
#endif // DEBUG_ALGORITHM
int Num = LeafNodes.Num();
const FVector& Start = LeafNodes[Num - 2].Bound.Origin;
const FVector& End = LeafNodes[Num - 1].Bound.Origin;
OpenList.Reset();
CloseSet.Reset();
OpenList.HeapPush({ Num - 2 , Num - 2, 0, FVector::Dist(Start, End) });
while (OpenList.Num() > 0) {
FAStarNode CurNode;
OpenList.HeapPop(CurNode, false);
if (CloseSet.Contains(CurNode.Index)) continue;
CloseSet.Add(CurNode.Index, { CurNode.Parent, CurNode.CurCost });
if (CurNode.Index == Num - 1) break;
for (TPair<int32, float>& Line : Graph[CurNode.Index]) {
if (CloseSet.Contains(Line.Key)) continue;
float CurCost = CurNode.CurCost + Line.Value;
OpenList.HeapPush({ Line.Key , CurNode.Index, CurCost, CurCost + FVector::Dist(LeafNodes[Line.Key].Bound.Origin, End) });
//Path2
#ifdef DEBUG_ALGORITHM
Count++;
#endif // DEBUG_ALGORITHM
FVector t;
if (!Octree->HitTestWithLine(LeafNodes[CurNode.Parent].Bound.Origin, LeafNodes[Line.Key].Bound.Origin, t)) {
CurCost = CloseSet[CurNode.Parent].Cost + FVector::Dist(LeafNodes[Line.Key].Bound.Origin, LeafNodes[CurNode.Parent].Bound.Origin);
OpenList.HeapPush({ Line.Key , CurNode.Parent, CurCost, CurCost + FVector::Dist(LeafNodes[Line.Key].Bound.Origin, End) });
}
}
}
#ifdef DEBUG_ALGORITHM
GEngine->AddOnScreenDebugMessage(0, 5.0f, FColor::Red, FString::Printf(TEXT("射线检测次数:%d"), Count));
#endif // DEBUG_ALGORITHM
}Lazy Theta*
Theta*在搜索的过程中做了太多射线检测,Lazy Theta* 利用 A*大多数节点弹出 OpenList 的时候远少于加入 OpenList 的次数,因此加入节点时默认所有的节点都不会碰撞到父节点,弹出时再判断是否真的不会碰撞。
void AMyOctreeActor::RunLazyThetaStar()
{
#ifdef DEBUG_ALGORITHM
int32 Count = 0;
#endif // DEBUG_ALGORITHM
int Num = LeafNodes.Num();
const FVector& Start = LeafNodes[Num - 2].Bound.Origin;
const FVector& End = LeafNodes[Num - 1].Bound.Origin;
OpenList.Reset();
CloseSet.Reset();
OpenList.HeapPush({ Num - 2 , Num - 2, 0, FVector::Dist(Start, End) });
while (OpenList.Num() > 0) {
FAStarNode CurNode;
OpenList.HeapPop(CurNode, false);
if (CloseSet.Contains(CurNode.Index)) continue;
FVector HitResult;
#ifdef DEBUG_ALGORITHM
Count++;
#endif // DEBUG_ALGORITHM
if (CurNode.bLazyTheta && Octree->HitTestWithLine(LeafNodes[CurNode.Parent].Bound.Origin, LeafNodes[CurNode.Index].Bound.Origin, HitResult)) {
continue;
}
else {
CloseSet.Add(CurNode.Index, { CurNode.Parent, CurNode.CurCost });
}
if (CurNode.Index == Num - 1) break;
for (TPair<int32, float>& Line : Graph[CurNode.Index]) {
if (CloseSet.Contains(Line.Key)) continue;
float CurCost = CurNode.CurCost + Line.Value;
OpenList.HeapPush({ Line.Key , CurNode.Index, CurCost, CurCost + FVector::Dist(LeafNodes[Line.Key].Bound.Origin, End) });
//Path2
CurCost = CloseSet[CurNode.Parent].Cost + FVector::Dist(LeafNodes[Line.Key].Bound.Origin, LeafNodes[CurNode.Parent].Bound.Origin);
OpenList.HeapPush({ Line.Key , CurNode.Parent, CurCost, CurCost + FVector::Dist(LeafNodes[Line.Key].Bound.Origin, End), 1 });
}
}
#ifdef DEBUG_ALGORITHM
GEngine->AddOnScreenDebugMessage(0, 5.0f, FColor::Red, FString::Printf(TEXT("射线检测次数:%d"), Count));
#endif // DEBUG_ALGORITHM
}路径平滑
最后往往对路线的选择没有那么高的要求,可以参考 Theta*的思路,对 A* 得到的结果进行平滑,这样碰撞检测的次数更少,我这里实测路径平滑得到的结果比 Theta*效果还好,可能是空间划分过度的不均匀导致的,因为原始的 Theta* 算法是在规则 2 维网格上的。
void AMyOctreeActor::RunSmoothPath()
{
#ifdef DEBUG_ALGORITHM
int32 Count = 0;
#endif // DEBUG_ALGORITHM
RunAStar();
int CurNode = LeafNodes.Num() - 1;
if (CloseSet.Contains(CurNode)) {
int ParentNode = CloseSet[CurNode].Parent;
while (ParentNode != LeafNodes.Num() - 2) {
FVector HitResult;
#ifdef DEBUG_ALGORITHM
Count++;
#endif // DEBUG_ALGORITHM
if (Octree->HitTestWithLine(LeafNodes[CurNode].Bound.Origin, LeafNodes[CloseSet[ParentNode].Parent].Bound.Origin, HitResult)) {
CloseSet[CurNode].Parent = ParentNode;
CurNode = ParentNode;
}
ParentNode = CloseSet[ParentNode].Parent;
}
CloseSet[CurNode].Parent = ParentNode;
}
#ifdef DEBUG_ALGORITHM
GEngine->AddOnScreenDebugMessage(0, 5.0f, FColor::Red, FString::Printf(TEXT("射线检测次数:%d"), Count));
#endif // DEBUG_ALGORITHM
}结果
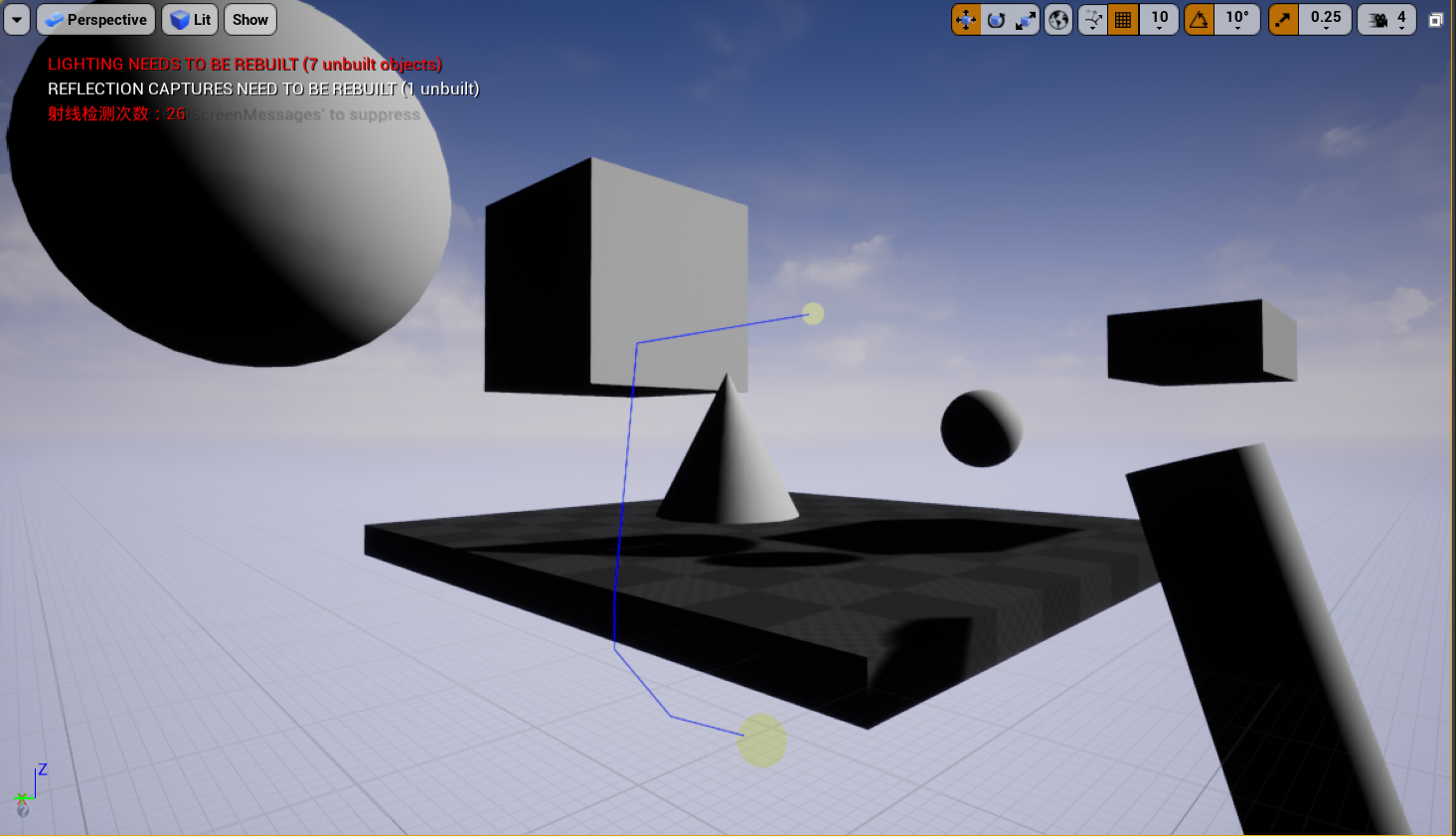
最后对比一下四种寻路算法的路径和射线测试的次数。
A*
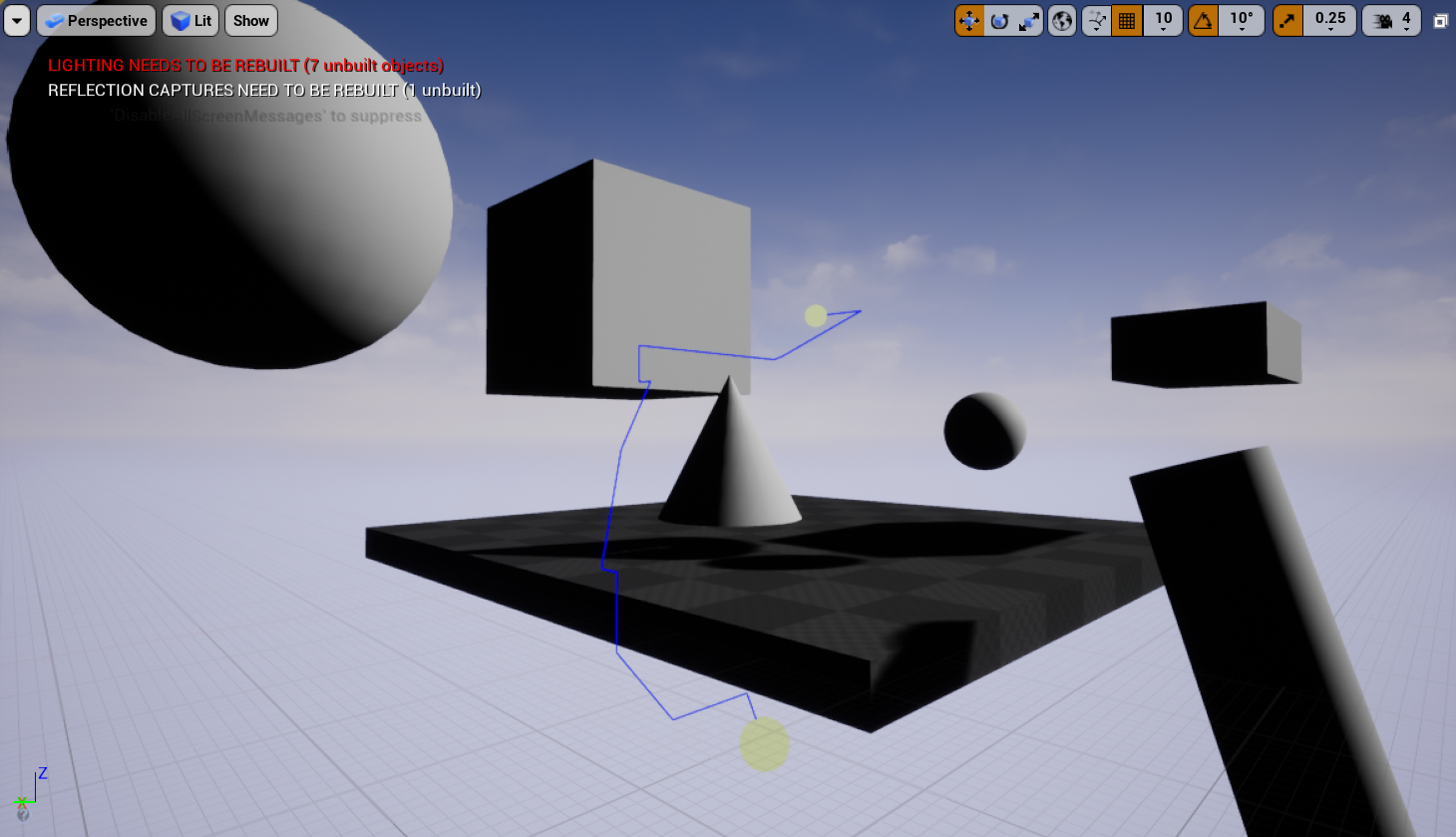
Theta*
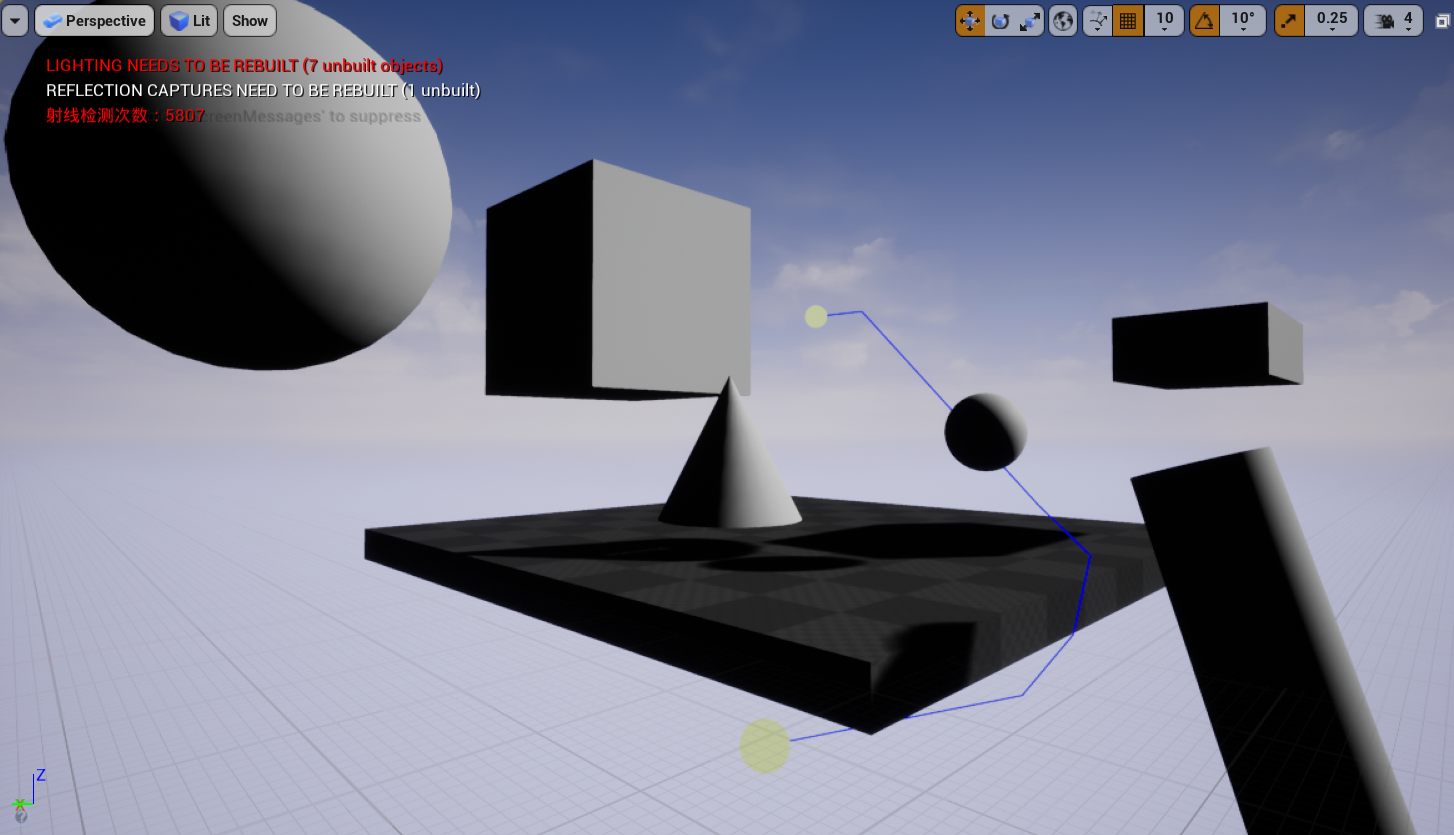
LazyTheta*
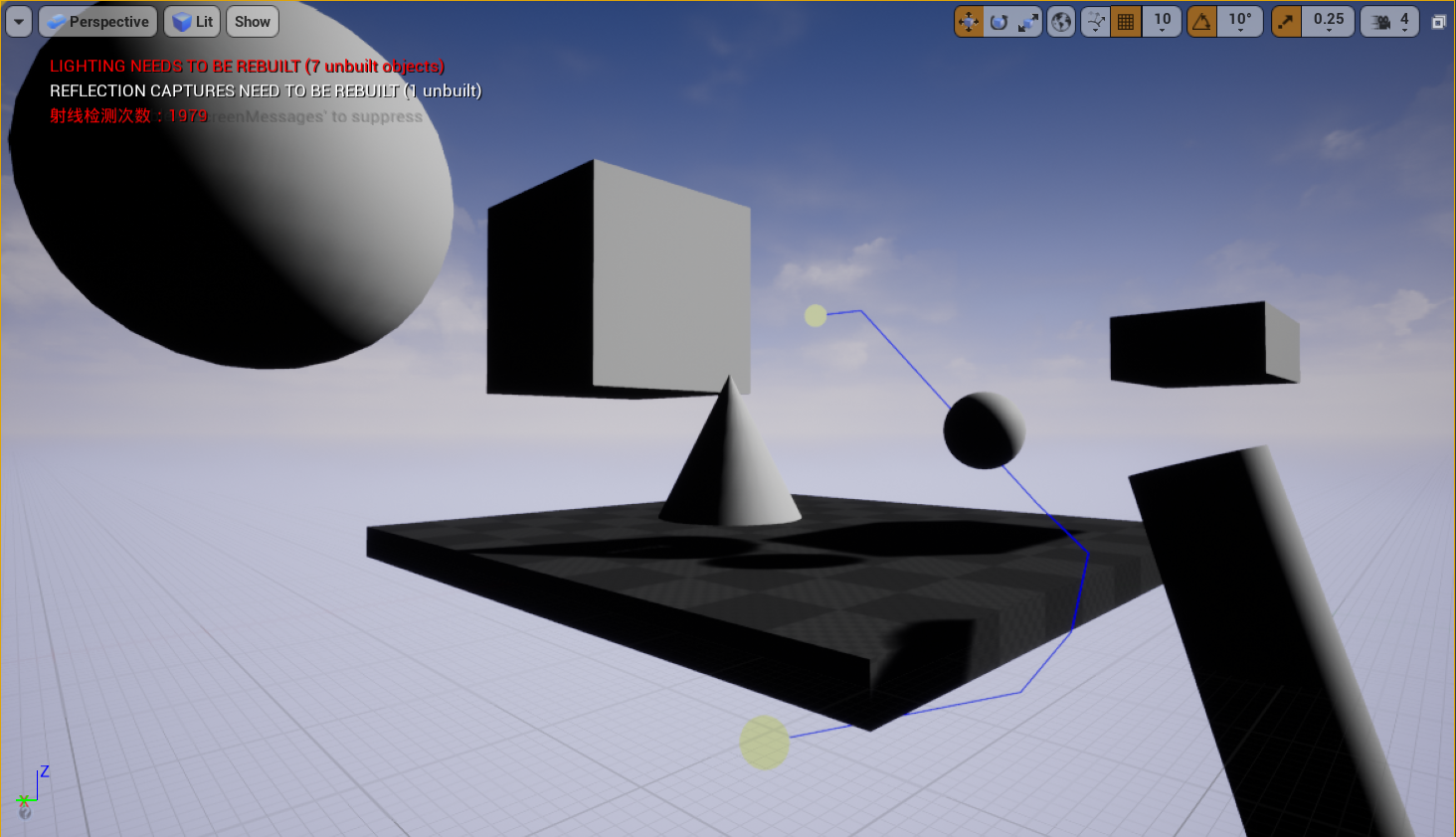
AStar+Smooth
代码涉及的 OctreeActor 和 Octree.h 下载。
MyOctree.zip
最后这棵树其实还有可以优化的地方比如在每个节点记录所有子节点的 Blocks 情况,可以在射线检测时加速判断,这个在 UE 源码中 FNode 中的 InclusiveNumElements 就是这样用的,我这里就没有加了,先这样。
0
暂无讨论